Chapter 1, Section 4
Math Topics – Blocks in Other Bases; Converting Between Base Ten and Other Bases
Elementary Education – Counting Games
Counting Games for Children
Children can do skip counting to emphasize counting patterns. Counting by tens (“ten twenty, thirty, forty….”) or by hundreds (“One hundred, two hundred….) emphasizes the base ten nature of our number system. You might remember skip counting by 2’s or 10’s when you were younger, like in this video, which talks about how to use unifix cubes in skip counting:
Skip counting can be done with larger skips as well! This video shows third-graders skip counting by 200’s so they can look for patterns: https://learn.teachingchannel.com/video/teaching-number-patterns
Counting Games for Adults: Bizz-Buzz for Base Systems
This game was adapted from a counting/drinking game! In this base systems version of the game, you cannot say the number of the base you are playing in. If we play Bizz-Buzz in base 5, we cannot say five. We count 1, 2, 3, 4, bizz, 1, 2, 3, 4, bizz bizz, 1, 2, 3, 4, bizz bizz bizz, etc. Instead of saying bizz five times, we say buzz.

Example 1 How would we count to 14 in Bizz-Buzz Base 5?
We would count 1, 2, 3, 4, bizz (instead of 5), 1, 2, 3, 4, bizz bizz (instead of ten), 1, 2, 3, 4.
Answer: 14 = 2 bizz and 4 more
Another way to write this answer is in table form, showing that we have said bizz twice, and then counted to 4 after that:
| Bizz | Ones |
| 2 | 4 |
Or, because Bizz is 5, we can write the table like this.
| 5’s | Ones |
| 2 | 4 |
We can write this answer as a number with a subscript of 5, to show we are in base 5: 245
Example 2 How would we count to 29 in Bizz-Buzz Base 5?
We would count up to buzz and then count to 4 more.
29 = 1 buzz and 4 more
Another way to write this answer is
| Buzz | Bizz | Ones |
| 1 | 0 | 4 |
Notice that in table form, we show 1 buzz, no bizzes, and 4 ones.
We can change the table to show 25’s and 5’s, since Buzz is 25 and bizz is 5:
| 25’s | 5’s | Ones |
| 1 | 0 | 4 |
We can write this answer as a number with a subscript of 5, to show we are in base 5: 1045
Question: If you count to 57 playing bizz-buzz, how many times would you say buzz? And then how many bizzes after that, and how many ones? How would you write that in base 5? Check your answer, here: https://koffenholley.survey.fm/bizz-buzz-for-57
Example 3 How would you count to 29 in Bizz-Buzz base 7?

In base 7, you would count 1, 2, 3, 4, 5, 6, bizz, 1, 2, 3, 4, 5, 6, bizz bizz, etc. To get to 29, we would have said bizz 4 times (since 4 × 7 = 28), and then 1 more.
Answer: 29 = 4 bizz and 1 more. We could also write 29 = 417.
Question: How would you play bizz buzz in base 8? How would you count up to 67? Check here to see if you are right: https://koffenholley.survey.fm/bizz-buzz-for-67
Base Five Blocks
Base five blocks represent the powers of five.
Units are 50 = 1
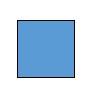
Rods are 51 = 5. Five units make one rod.
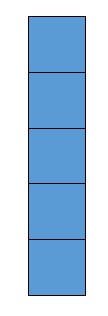
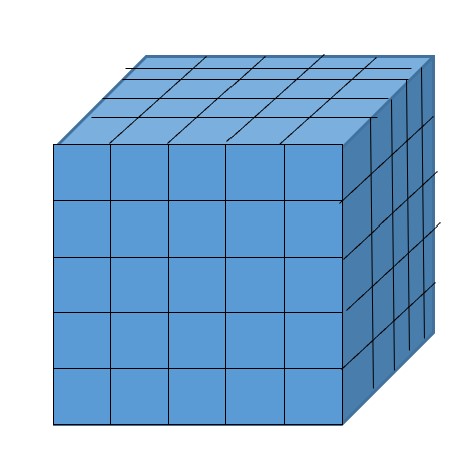
Flats (squares) are 52 = 25. Five rods make one flat.

Cubes are 53 = 125. Five flats make one cube.
| cubes | flats | rods | units |
| 53 | 52 | 51 | 50 |
| 125 | 25 | 5 | 1 |
Notice that we read 53 as “five cubed,” and it makes the shape of a cube. we read 52 as “five squared,” and it makes the shape of a square. The rods are one dimensional.
The base 5 blocks also relate to Bizz Buzz, in that the rods are the same as a bizz, and the flats are the same a buzz.
Example 4 Make 2135 using base five blocks, then convert into base ten.
Since 2135 is a number in base 5, each place value is in base 5.
| 52 | 51 | 50 |
| 25 | 5 | 1 |
| 2 flats | 1 rod | 3 units |
This means that we can make a model of 2135 using two base 5 flats, 1 rod, and 3 units.
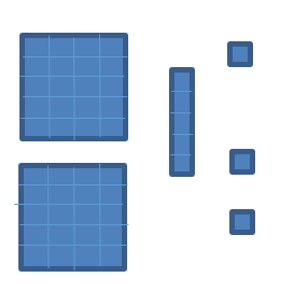
Two base 5 flats are worth 25 + 25. One rod is worth 5, and three units is 3. So we have: 2135 = 25 + 25 + 5 + 3 = 58. We could also write this as:
| 52 | 51 | 50 |
| 25 | 5 | 1 |
| 2 flats 2 x 25 | 1 rod 1 x 5 | 3 units 3 x 1 |
Example 5 Make 21425 using base five blocks, then convert into base ten.
Since 21425 is a number in base 5, each place value is in base 5. We have 2 cubes, 1 flat, 4 rods and 1 unit.
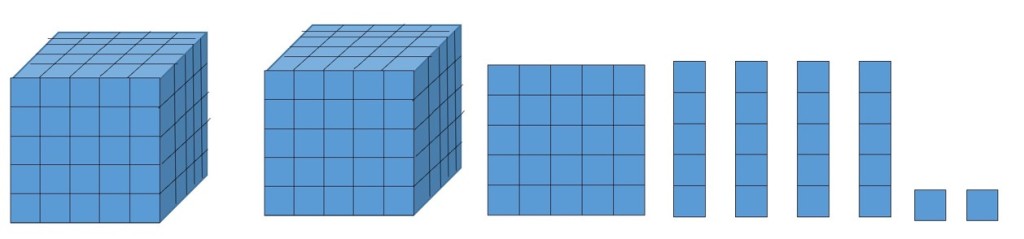
| 53 | 52 | 51 | 50 |
| 125 | 25 | 5 | 1 |
| 2 cubes 3 x 125 | 1 flat 1 x 25 | 4 rods 4 x 5 | 2 units 2 x 1 |
This gives us 21425 = (3 × 125) + (1 × 25) + (4 × 5) + (2 × 1) = 422.
Example 6 Convert the number 81 into base 5, using base 5 blocks.
Note that now we are going in the other direction. 81 is not a base 5 number. We need to figure out how to get it into base 5.
Start by thinking how many base 5 flats we would need to get as close as possible to a value of 81. If we use 3 flats, each worth 25, we will have 3 × 25 = 75, which is close to 81. If we use 4 flats, we will have 4 × 25 = 100, which is too high. After we get three flats out, we have 81 – 75 = 6 left, so we would need one rod, worth 5, plus 1 unit.
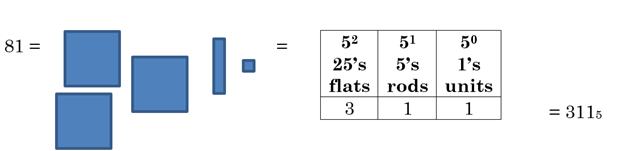
This means that 81 is equal to the base 5 number 3115.
Example 7 Convert the number 127 into base 5, using base 5 blocks.
127 is a much higher number, so now we can start by thinking how many base 5 cubes we would need to get as close as possible to a value of 127. A cube is worth 125, so we would only need one, with two units left over.
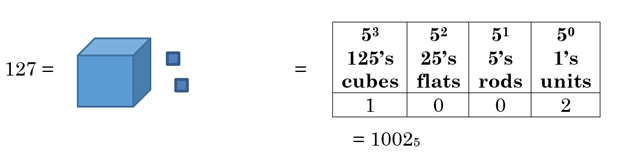
This means that 127 is equal to the base 5 number 10025. Notice that we use the zeros to show that no flats or rods are needed.
Question: How would you convert 272 into base 5, using base 5 blocks? Tip: start with cubes! Once you think you have it, check here: https://koffenholley.survey.fm/272-into-base-5
Converting between Other Bases
To convert between bases, we can think of the base blocks, or use a table showing the place values. For example, if we want to convert between base 5 and base 10, we can use base 5 blocks, or we can use a table of base 5 place values. If we want to convert between base 7 and base 10, we can use base 7 blocks, or we can use a table of base 7 place values.

Example 8 Convert 2347 into base 10.
The number 2347 is already in base 7. We can tell because of the little 7 subscript on the number. Since 2347 is in base 7, we can place the number into the base 7 place values table:
| 72=49’s | 71=7’s | 70=1’s |
| 2 | 3 | 4 |
| 2×49 | 3×7 | 4×1 |
We can also picture this as 2 base-7 flats (each worth 49), 3 rods (each worth 7) and 4 units (each worth 1).
Thus, 2347 = (2 × 49) + (3 × 7) + (4 × 1) = 98 + 21 + 4 = 123.
Answer: 2347 = 123
Example 9 Convert 207 into base 7.
The number 207 is not in base 7. We can tell because there is no 7 subscript on the number. Since 207 is not in base 7, we cannot place the number into the base 7 table. Instead, we must figure out what will go into the table to get 207.
| 72=49’s | 71=7’s | 70=1’s |
| ? | ? | ? |
| ?×49 | ?×7 | ?×1 |
= 207
We start with the 49’s place, to see how many 49’s would fit into 207. You can also imagine this as using base-7 flats to make as close as possible to 207. Divide: 207 ÷ 49 = 4.224…, so we know we will need 4 flats, and 49 × 4 = 196.
| 72=49’s | 71=7’s | 70=1’s |
| 4 | ? | ? |
| 4×49 = 196 | ?×7 | ?×1 |
207 – 196 = 11, So now we complete the table by figuring out how many 7’s and ones (base 7 rods and units) we need to make 11.
| 72=49’s | 71=7’s | 70=1’s |
| 4 | 1 | 4 |
| 4×49 = 196 | 1×7 = 7 | 4×1 = 4 |
Answer: 207 = 4147
Converting Bases Summary
Converting from a different base to base 10.
- Step 1: Make a place value table for powers of the different base.
- Step 2: Place the number in the table because it is in that base.
- Step 3: Multiply the digits by each place value and add.
Converting from base ten to a different base.
- Step 1: Make a place value table for powers of the different base.
- Step 2: Place the number outside the table because it is not in that base.
- Step 3: Divide the number you have by the first place value. Multiply and subtract to see what is left. Repeat with the next place value until done!
Notice that for both sets of steps, we never make a base ten place value table. The place value table is always for the “different” base. We automatically already think in base ten, so we don’t need to write a base ten table. We also don’t write a subscript of 10 on our numbers.
Example 10 Convert 27312 into base 10.
| 122=144’s | 121=12’s | 120=1’s |
- Step 1: Make a place value table for powers of the different base, in this case, base 12.
- Step 2: Place the number in the table because it is in that base.
- Step 3: Multiply the digits by each place value and add.
| 122=144’s | 121=12’s | 120=1’s |
| 2 | 7 | 3 |
| 2×144 = 288 | 7×12 = 84 | 3×1 = 3 |
288 + 84 + 3 = 375
The answer is 375.
Example 11 Convert 394 into base 12.
- Step 1: Make a place value table for powers of the different base, base 12.
- Step 2: Place the number 394 outside the table because it is not in that base.
- Step 3: Divide the number you have by the first place value, 144: 394 ÷ 144 = 2.736, so we know to put 2 in the first place value … So far we have:
| 122=144’s | 121=12’s | 120=1’s |
| 2 | ? | ? |
| 2 × 144 |
= 394
Multiply and subtract to see what is left. 2 × 144 = 288, so we have 394 – 288 = 106 left.
Divide the number you have left by the next place value, 12.
106 ÷ 12 = 8.833, so we place 8 in the 12’s column. Now we have:
| 122=144’s | 121=12’s | 120=1’s |
| 2 | 8 | ? |
| 2 × 144 288 | 8 × 12 96 |
= 394
Again, multiply and subtract to see what is left. 8 × 12 = 96, so we have 106 – 96 = 10 left.
This last amount left goes in the ones place.
| 122=144’s | 121=12’s | 120=1’s |
| 2 | 8 | 10 |
| 2 × 144 288 | 8 × 12 96 | 10 × 1 10 |
288 + 96 + 10 = 394
Notice that in base 12, we are allowed to have up to the number 11 in any place value column! Think about the Mayans, who could have up to 19 in any given place value. In our system, base ten, we can only have up to 9 in a place value.
However, we cannot write 281012, because that would seem like we were trying to write
| 123 =1728’s | 122 = 144’s | 121 =12’s | 120 = 1’s |
| 2 | 8 | 1 | 0 |
| 2 × 1728 3456 | 8 × 144 1152 | 1 × 12 12 | 0 × 1 0 |
= 4,620, not 394 as intended!
So instead, in base 12, we use a T to stand for ten and an E for eleven. (You can actually use any letters you like, as long as you note what the letters stand for.)
So we write 394 = 28T12 for our answer.
Very Quick Questions: If you want to convert 124 8 into base 10, do you make base 8 place values or base ten values? Do you place the number in the place values table or outside of it?
If you want to convert 217 into base 8, do you make base 8 place values or base ten values? Do you place the number in the place values table or outside of it? https://koffenholley.survey.fm/very-quick-converting-questions Note: you do not have to actually convert the two numbers, this question is just to make sure you start out correctly!
Binary, Base 2

In base 2, numbers are written only with ones and zeros. This is because any base system will always have numbers from zero up to one less than the base.
- In base 5, we can write numbers from 0 to 4 in any given place value.
- In base 10, we can write numbers from 0 to 9 in any given place value.
- In base 2, we can write numbers from 0 to 1 in any given place value.
Binary is the language of electricity, since an electrical impulse is either on (1) or off (0). Binary is the deepest language inside a computer. The number 11012 is on-on-off-on.
Example 12 Convert 10111012 into base 10.
| 26 64 | 25 32 | 24 16 | 23 8 | 22 4 | 21 2 | 20 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 × 64 | 0 × 32 | 1 × 16 | 1 × 8 | 1 × 4 | 0 × 2 | 1 × 1 |
- Step 1: Make a place value table for powers of the different base, in this case, base 2.
- Step 2: Place the number in the table because it is in that base.
- Step 3: Multiply the digits by each place value and add: 64+0+16+8+4+0+1 = 93
Example 13 Convert 42 into binary (base 2).
- Step 1: Make a place value table for powers of the different base, in this case, base 2.
- Step 2: Place the number outside the table because it is not in that base.
| 25 32 | 24 16 | 23 8 | 22 4 | 21 2 | 20 1 |
| ? | ? | ? | ? | ? | ? |
| ? × 32 | ? × 16 | ? × 8 | ? × 4 | ? × 2 | ? × 1 |
=42
Step 3: Divide 42 by the first place value, 32 and subtract to get the remainder: 32 goes into 42 once, with 10 left over. We can also write 42 ÷ 32 = 1.3125, and 42 – 32 = 10.
| 25 32 | 24 16 | 23 8 | 22 4 | 21 2 | 20 1 |
| 1 | ? | ? | ? | ? | ? |
| 1 × 32 | ? × 16 | ? × 8 | ? × 4 | ? × 2 | ? × 1 |
How did we know to start with the 25 column this time, and not 26?
Answer: 64 is too large. If we had a 1 in the 64’s column, we would have a result much larger than 42. (Also, 42 ÷ 64 gives us a fraction less than 1.)
To make the 10 more that we need, we can use an 8 and a 2:
| 25 32 | 24 16 | 23 8 | 22 4 | 21 2 | 20 1 |
| 1 | 1 | 1 | |||
| 1 × 32 | ? × 16 | 1 × 8 | ? × 4 | 1 × 2 | ? × 1 |
We cannot make the 10 more by putting, say, a 5 in the 2’s column, because we cannot have more than 1 in any column.
Now will fill the rest of the table with zeros, and we’re done.
| 25 32 | 24 16 | 23 8 | 22 4 | 21 2 | 20 1 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 × 32 | 0 × 16 | 1 × 8 | 0 × 4 | 1 × 2 | 0 × 1 |
(1 × 32) + (0 × 16) + (1 × 8) + (0 × 4) + (1 × 2) + (0 × 1) = 42
It is extremely important to check your answers. If you find there is a different answer from what you got, don’t erase yours! Instead, put a light cross out through yours and then see if you can figure out how to get the correct answer; ask in class discussion if you can’t. Do not copy the answers below. Do your own work, and show it next to each problem.